Kreativita nie je len o talente, či intuícii, ale aj o exaktných pojmoch. Jedným takým je zlatý rez - častý pomer proporcionality objektov objavujúci sa, ako v prírode, tak i v umeleckej tvorbe. Praktické uplatnenie však dlhodobo nachádza aj v dizajne.

Grécke písmeno „fí“ (v gréckej abecede písané veľkým Φ a malým φ) v matematike popisuje jedno veľmi zaujímavé iracionálne číslo. Je odvodené od približného výsledku geometrickej úlohy, ktorá znie: rozdeliť úsečku na dve časti tak, aby pomer dlhšej časti ku kratšej časti bol rovnaký ako pomer dĺžky celej úsečky k dlhšej časti. Teda, ak x je dĺžka úsečky, a je jej dlhšia časť a b je jej kratšia časť, musí platiť a/b = x/a, čiže aj:
a/b = (a+b)/a
Tento vzťah má po zjednodušení na kvadratickú rovnicu dva výsledky (korene) a jedným z nich je číslo s približnou hodnotou 1,618033, nazývané aj „zlatý rez“, či „zlatý podiel“ (lat. sectio divina).
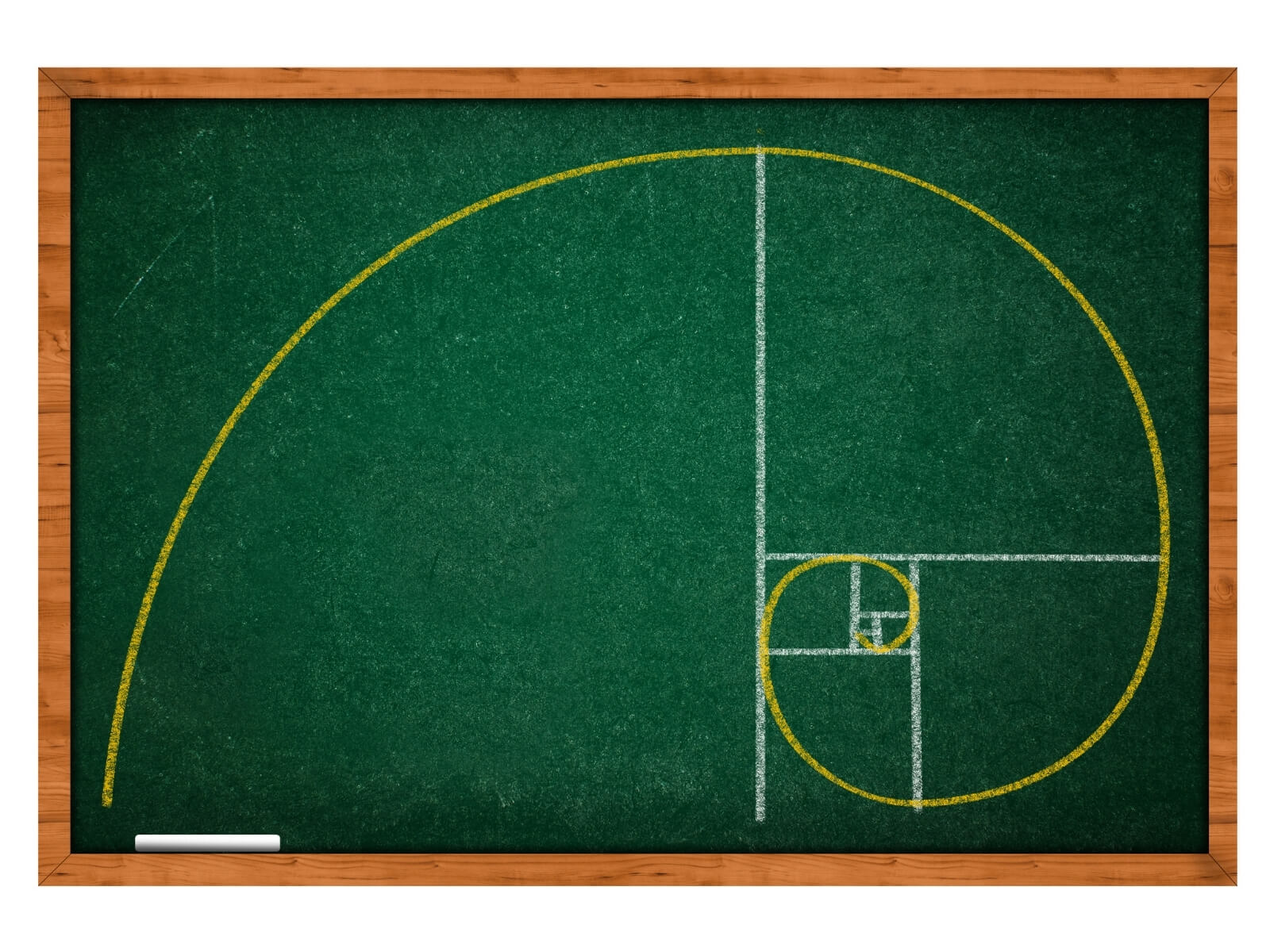
Prečo zlatý? Ukázalo sa, že proporcionalita v pomeroch blízkych fí sa nezriedka vyskytuje nielen v obdivuhodných prírodných štruktúrach, ale je typická aj pre mnohé ľudské umelecké výtvory, často považované za esteticky hodnotné, ak nie priam klasické diela. Domnienky niektorých vedcov dokonca siahajú až tak ďaleko, že naznačujú spojitosti medzi zlatým pomerom a akýmsi vrodeným zmyslom pre krásu.

História
Kedy presne bolo fí objavené nie je známe. Za svoje označenie vďačí gréckemu sochárovi a matematikovi menom Feidias (Phidias, 5. storočie p.n.l.), ktorý tento oku lahodiaci pomer používal pri tvorbe svojich sôch. Analýza rozmerov egyptských pyramíd však naznačuje, že zlatý rez bol pravdepodobne prakticky využívaný už pri ich stavbe v treťom tisícročí p.n.l.
Fí bolo v stredoveku hojne používané pri kalkuláciách spojených s pravidelnými päťuholníkmi a pentagramami, ako na európskom kontinente, tak i v arabskom svete. V roku 1202 sa na území terajšieho Talianska objavil manuskript Liber Abaci (Kniha výpočtov) a jeho autorom bol matematik Leonardo z Pisy, posmrtne známy pod menom Fibonacci. Azda najpamätnejšia sekcia manuskriptu pojednáva o hypotetickej populácii králikov, množiacej sa mesačne podľa systematických pravidiel.
Aby Fibonacci vypočítal koľko králikov bude mať populácia po období jedného roku, popísal číselný rad, ktorý začína číslami 0 a 1. Každý ďalší člen radu pribúda tak, že sa sčítajú dva predošlé členy, teda: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... Čísla Fibonacciho sekvencie majú veľa neobyčajných charakteristík a jednou z nich je, že pri delení dvoch susediacich čísel (väčšieho menším) je výsledok vždy veľmi blízky fí. Tento fakt zrejme samotnému Fibonaccimu unikol, no postupne si ho všimlo viacero slávnych matematikov, okrem iných Edouard Lucas (ten rad pomenoval po Fibonaccim) i Johannes Kepler. Lucas tiež od Fibonacciho radu odvodil podobný rad (2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, ...), v ktorom je podiel susediacich taktiež fí.
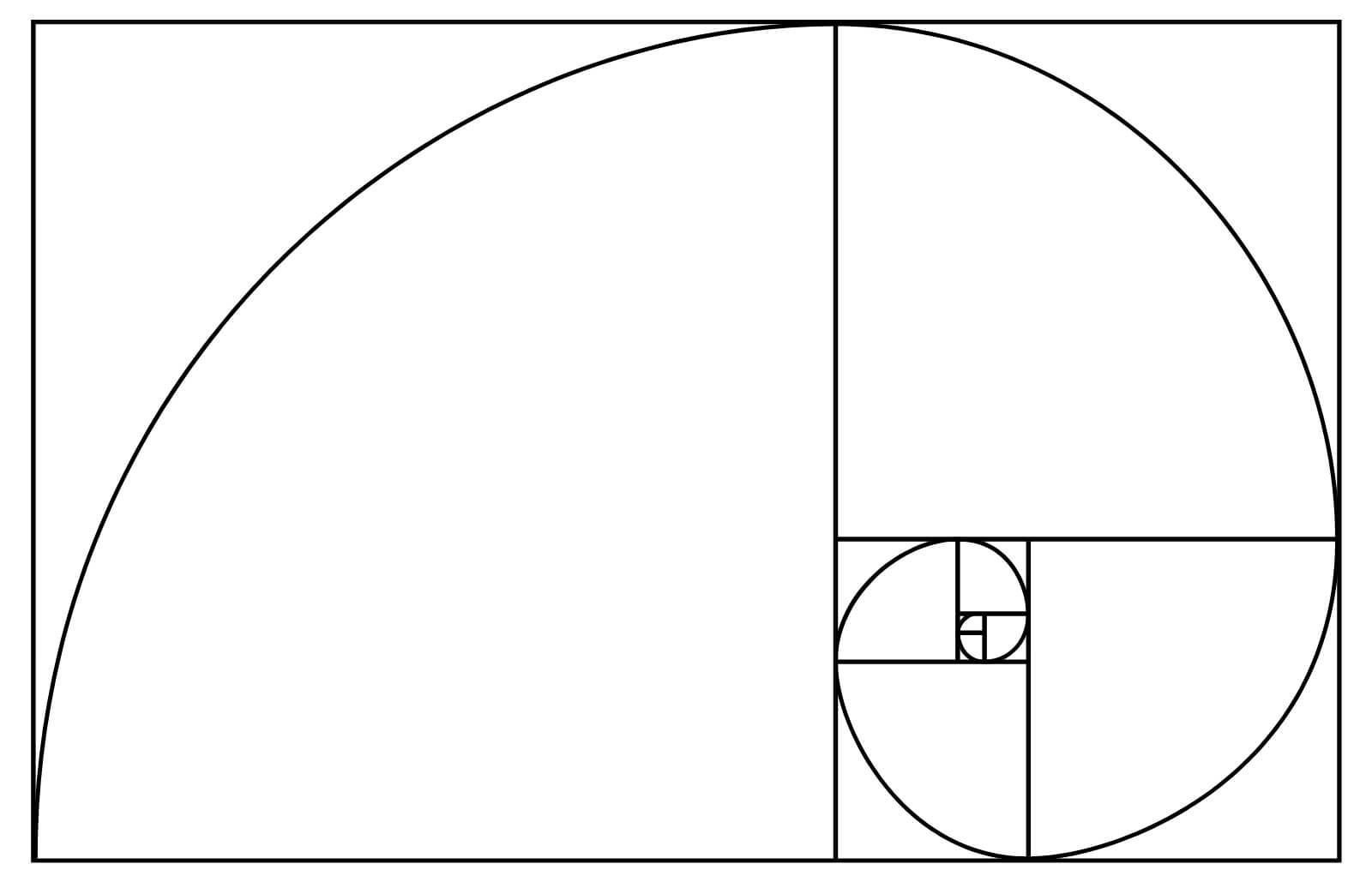
Keď sa čísla Fibonacciho radu umocnia na druhú, vzniknú štvorce. Tieto štvorce je následne možné uložiť spôsobom, aby sa navzájom dopĺňali tak, že budú plošnou demonštráciou zlatého rezu. V každom zo štvorcov je tiež možné narysovať presný oblúk spájajúci dva protiľahlé vrcholy. Jeho polomer je príslušné Fibonacciho číslo a stred má v jednom z vrcholov príslušného štvorca. A ak sú oblúky narysované tak, že každý začína v bode, kde končí ten predchádzajúci (z pohľadu poradia štvorcov podľa Fibonacciho radu) vznikne tvar špirály – „zlatej špirály“.
Fascinácia zlatým rezom a Fibonacciho radom pokračuje dodnes, známe sú napríklad takzvané Penroseove aperiodické obklady, diela moderného holandského maliara Pieta Mondriana, či architektúra Le Corbusiera.

Príklady zlatého rezu (a Fibonacciho sekvencie)
Ríša prírody ponúka mnoho úžasných a nečakaných príkladov pre utvorenie si konkrétnejšej predstavy o abstraktných matematických konceptoch zlatého rezu a Fibonacciho radu.
- Počet lupeňov kvetov je veľmi často identický s niektorým z čísel Fibonacciho radu a aj pri druhoch, ktoré tvoria výnimku (ako fuksie) je počet lupeňov členom Lucasovho radu.

- Usporiadanie semien koncentrovaných v strede kvetu slnečnice, alebo echinacey vykazuje tvar zlatej špirály.

- Štruktúra šišiek borovice pri pohľade zospodu taktiež odhaľuje usporiadanie jednotlivých segmentov v tvare známej špirály.

- Inak tomu nie je ani pri hlávkach karfiolu, či brokolice odrody romanesco.

- Fibonacciho číselnú sekvenciu je možné sledovať aj pri usporiadaní listov rastlín na stopke a zdá sa byť optimálnym riešením polohy listov tak, aby si navzájom netienili. Podobne tiež pri rozkonárovaní stromov na úrovniach smerom od kmeňa nahor často pribúdajú vetvy tak, že celkové počty sú 2, 3, 5, 8, 13, atď.
- Mušle slimákov a morských živočíchov sú ďalším z radu príkladov zlatej špirály.

- Aj tvary hurikánov na záberoch z družice a špirálových galaxií odfotených pomocou teleskopu dokumentujú výskyt toho istého vzoru, tentoraz v anorganickej forme.
- Proporcionalita ľudskej tváre, funkčných častí tiel živočíchov, pomer počtu samičiek a samčekov v kolóniách hmyzu, stavba niektorých vnútorných orgánov, či dokonca štruktúra DNA – všetky z týchto organických celkov vykazujú väčšiu, či menšiu spojitosť so zlatým pomerom fí.
Jednoduchosť a krásu rozloženia objektu na menšie časti v pomere približne 1,618 nie je problém vystopovať ani v dielach maliarov, sochárov a architektov. V Botticelliho obraze Zrodenie Venuše je takto znázornené telo bohyne, Michelangelo v Stvorení Adama zvolil zlatý pomer medzi časťami obrazu vymedzenými hlavným postavám scény a v Seuratovom majstrovskom diele Kúpanie v Asnieres sú takto dômyselne rozložené všetky sekcie maľby. Da Vinciho i Dalího spracovania námetu poslednej večere, portréty Mony Lisy, Dámy s hranostajom i Dievčaťa s perlovou náušnicou, či moderné abstraktné diela Mondriana nasledujú rovnaký kompozičný princíp.

Aj antický ideál krásy zhmotnený v sochách postáv ľudí i bohov na mnohých príkladoch dokladuje zlatý pomer – tentokrát dolnej časti ľudského tela k hornej, s deliacou líniou presne vo výške pupka, ktorý je vďaka obnaženiu postáv často viditeľný.
Aplikácia zlatého rezu na architektonické prvky svetoznámych budov má, aj vďaka už spomínaným egyptským pyramídam, za sebou azda najdlhšiu históriu. Architekti sa tohto pomeru nestránili v žiadnom období a jeho prítomnosť tak badať v typických stavbách takmer každého zo slohov – Parthenón, Taj Mahal, Notre-Dame, Villa Stein sú len niekoľkým z mnohých.

Zlatý rez v dizajne
Súčasný prístup ku kompozícii v dizajne sa neriadi žiadnymi pevne danými pravidlami. Ani zlatý rez nie je samozrejmou zárukou atraktivity, no ako inšpirácia pre určité fundamentálne praktiky pri rozvrhovaní hrubej štruktúry návrhu, mriežky v pozadí, hierarchie prvkov a podobne môže skvele poslúžiť. Všetko sú to veci, ktoré dizajnér nikdy nenavrhuje s cieľom, aby si ich všimol konečný užívateľ, či spotrebiteľ. Zlatý pomer má tvoriť neviditeľný organizačný princíp, ktorý je skôr pociťovaný ako vnímaný rozumom.
Jedným dobrým orientačným faktorom je celková veľkosť dizajnovaného objektu – čím je väčší (nábytok, billboard), tým viac záleží i na detailoch kompozície.

Spôsobov, ako uvedené zásady implementovať v praxi, je niekoľko. Usporiadanie prvkov a výpočet ich presných dimenzií sa môže realizovať tak, aby výsledné pomery hlavných rozmerov boli približne rovné fí. Uplatnenie sa iste osvedčí vo webdizajne pri dvojstĺpcovom zobrazení hlavného obsahu a bočného panelu menu, no koncepcia zobrazenia elementov v rámci týchto celkov môže byť identická.
Plošný sled štvorcov čísel Fibonacciho radu môže byť zasa vhodným usmernením pre dodržanie intervalov voľného miesta („whitespace“) s cieľom zachovania lepšej prehľadnosti a čitateľnosti obsahu.
Trasovanie zlatej špirály ako hlavného prúdu obsahu, prirodzene navádzajúceho zrak smerom do jej centra, má potenciál zachytiť a upútať pozornosť nenásilným spôsobom. Ak sú všetky kľúčové prvky umiestnené popri línii spontánneho víru špirály, je ťažké si ich nevšimnúť. Prirodzene, obsah smerom do centra hustne, preto je dôležité myslieť aj na zrozumiteľnosť, farebnú schému a podobne.
„Pravidlo tretín“ je aplikovateľné pri rozvrhovaní kombinácie obrázkov a textu, obyčajne titulku. Využíva druhý z koreňov riešenia kvadratickej rovnice zlatého rezu, ktorým je 0,618033. Rozdelenie dizajnu na tri sekcie v pomere 1:0,618:1 vertikálne a tri sekcie v tom istom pomere horizontálne vytvoria mriežku a v miestach, kde sa jej pomyselné deliace línie pretínajú je vhodné umiestniť prvky, na ktoré sa kladie dôraz.
„Zlaté kružnice“, čiže kružnice s priemerom čísel Fibonacciho radu, sú uplatniteľné pri grafickej príprave loga na dosiahnutie harmónie medzi rôznymi tvarmi, hranatými i oblejšími. Veľmi pekné výtvory môžu vzniknúť aj kreatívnym spájaním takýchto kružníc do nových sústav, ich vzájomným prekladaním a prelínaním.


 SK
SK 
